Gsyfuy

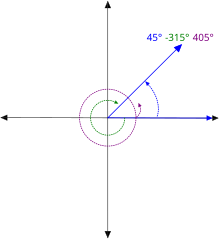
45度的3個同界角

在幾何學中，同界角（英语：Coterminal angles）是指兩個有向角有不同角度量值，但共用同一個起始邊與終邊，即共享相同的始邊和終邊的角度，但擁有不同的旋轉量，就稱為同界角^[1]。同界角擁有相同的三角函數值，因此三角函數具有周期性。每個角皆有無限多個同界角，其量值可以為負，但必須是一個實數。

性質

正轉和逆轉都可以得到相同的角，但他們擁有不同的旋轉量，圖中為45度和─315度

每個同界角皆差360度，換句話說，每360度就會出現一個同界角^[2]。每個同界角兩邊的向量內積與外積皆有相同的值。此外，任何角都可以找到最小正同界角和最大負同界角。

同界角可以如下定義：

1. 若有兩個角有相同的始邊與終邊，則兩個角互為同界角


2. 若兩角相差360度的整數倍則兩個角互為同界角

同界角存在關係式：

θ1−θ2=360∘k,k∈Z{displaystyle theta _{1}-theta _{2}=360^{circ }k,,kin mathbb {Z} }

亦可寫為：

θ1−θ2=2kπ,k∈Z{displaystyle theta _{1}-theta _{2}=2kpi ,,kin mathbb {Z} }

或：

sin⁡θ1−sin⁡θ2=0{displaystyle sin theta _{1}-sin theta _{2}=0}

cos⁡θ1−cos⁡θ2=0{displaystyle cos theta _{1}-cos theta _{2}=0}

與三角函數關係

從三角函數的周期可以發現，每間隔2π{displaystyle 2pi }就會找到相同高度的點，該點即為同界角的三角函數值。

從反三角函數圖形得知反餘弦必得到最小正同界角，而反正弦則有可能得到最小正同界角或最大負同界角

從三角函數的诱导公式可以得知同界角的存在，下表指出，任何三角函數，只要位移為2π{displaystyle 2pi }，就會得到相同的函數值，因此θ{displaystyle theta }與θ+2π{displaystyle theta +2pi }互為同界角。

移位 π2{displaystyle {frac {pi }{2}}}	移位 π{displaystyle pi } tan{displaystyle tan } 和 cot{displaystyle cot } 的周期	移位 2π{displaystyle 2pi } sin{displaystyle sin }、cos{displaystyle cos }、csc{displaystyle csc } 和 sec{displaystyle sec } 的周期
sin⁡(θ+π2)=+cos⁡θcos⁡(θ+π2)=−sin⁡θtan⁡(θ+π2)=−cot⁡θcot⁡(θ+π2)=−tan⁡θsec⁡(θ+π2)=−csc⁡θcsc⁡(θ+π2)=+sec⁡θ{displaystyle {begin{aligned}sin(theta +{tfrac {pi }{2}})&=+cos theta \cos(theta +{tfrac {pi }{2}})&=-sin theta \tan(theta +{tfrac {pi }{2}})&=-cot theta \cot(theta +{tfrac {pi }{2}})&=-tan theta \sec(theta +{tfrac {pi }{2}})&=-csc theta \csc(theta +{tfrac {pi }{2}})&=+sec theta end{aligned}}}	sin⁡(θ+π)=−sin⁡θcos⁡(θ+π)=−cos⁡θtan⁡(θ+π)=+tan⁡θcot⁡(θ+π)=+cot⁡θsec⁡(θ+π)=−sec⁡θcsc⁡(θ+π)=−csc⁡θ{displaystyle {begin{aligned}sin(theta +pi )&=-sin theta \cos(theta +pi )&=-cos theta \tan(theta +pi )&=+tan theta \cot(theta +pi )&=+cot theta \sec(theta +pi )&=-sec theta \csc(theta +pi )&=-csc theta end{aligned}}}	sin⁡(θ+2π)=+sin⁡θcos⁡(θ+2π)=+cos⁡θtan⁡(θ+2π)=+tan⁡θcot⁡(θ+2π)=+cot⁡θsec⁡(θ+2π)=+sec⁡θcsc⁡(θ+2π)=+csc⁡θ{displaystyle {begin{aligned}sin(theta +2pi )&=+sin theta \cos(theta +2pi )&=+cos theta \tan(theta +2pi )&=+tan theta \cot(theta +2pi )&=+cot theta \sec(theta +2pi )&=+sec theta \csc(theta +2pi )&=+csc theta end{aligned}}}

另外，從簡單的三角方程中，也可以找到同界角，例如：

考慮方程cos⁡(θ)=k,θ{displaystyle cos(theta )=k,,,theta }有無限多組解，其中arccos⁡(k){displaystyle arccos(k)}為一個解且為最小正同界角，其餘解皆與arccos⁡(k){displaystyle arccos(k)}或是-arccos⁡(k){displaystyle arccos(k)}互為同界角。

但是有例外，如正切和餘切，由於其週期不為360度，如正切函數的周期為180度（即π{displaystyle pi }），因此相同的函數值未必互為同界角。

參見

• 角


• 角度


• 三角函數

參考文獻

1. 
   ^ Neal, Karla V.; R. David Gustafson, Jeffrey D. Hughes. Coterminal angles. Precalculus, 1st ed.. Cengage Learning. : 第412頁. ISBN 1133712673.  引文使用过时参数coauthors (帮助)
   


2. 
   ^ Slavin, Steve; Ginny Crisonino. Circle. Wiley Self-Teaching Guides第 155 卷. John Wiley & Sons. 2004-10-28: 第90頁. ISBN 0471680192.  引文使用过时参数coauthors (帮助)