平稳过程 目录 定義 範例 广义平稳(弱平穩) 参见 导航菜单
随机过程信号处理
数学聯合機率分佈数学期望方差白噪声AWGN铙钹白噪声时间序列分析经济学趋势离散时间Bernoulli scheme伯努利过程![]()
![]()
![]()
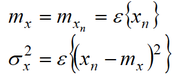 信号处理矩连续随机过程数学期望相关线性时不变线性时不变系统滤波器线性算子循环矩阵特征函数傅里叶级数复数指数函数频域信号处理
信号处理矩连续随机过程数学期望相关线性时不变线性时不变系统滤波器线性算子循环矩阵特征函数傅里叶级数复数指数函数频域信号处理
在数学中,平稳过程(英语:Stationary process),又稱严格平稳过程(英语:Strict(ly) stationary process)或強平穩過程(英语:Strong(ly) stationary process)是一種特殊的隨機過程,在其中任取一段期間或空間(t=t1−tk{displaystyle t=t_{1}-t_{k}})裡的聯合機率分佈,與將這段期間任意平移後的新期間(t=t1+τ−tk+τ{displaystyle t=t_{1}+tau -t_{k}+tau })之聯合機率分佈相等。这样,数学期望和方差这些参数也不随时间或位置变化。
例如,白噪声(AWGN)就是平稳过程,铙钹的敲击声是非平稳的。尽管铙钹的敲击声基本上是白噪声,但是这个噪声随着时间变化:在敲击前是安静的,在敲击后声音逐渐减弱。
在时间序列分析中稳态作为一个工具使用,在这里原始数据经常被转换为平稳态,例如经济学数据经常随着季节或者价格水平变化。如果这些过程是平稳过程与一个或者多个呈现一定趋势的过程的线性组合,那么这些过程就可以表述为趋势平稳。将这些数据进行转换保留平稳数据用于分析的过程称为解趋势(de-trending)。
采样空间也是离散的离散时间平稳过程称为Bernoulli scheme,离散采样空间中每个随机变量可能取得 N'个可能值中的任意一个。当 N = 2 的时候,这个过程叫做伯努利过程。
目录
1 定義
2 範例
3 广义平稳(弱平穩)
3.1 二阶平稳过程
4 参见
定義
如果有一個訊號x對於所有k都滿足以下條件,則它就是一個平穩過程。
![]()
也就是說,x[n]和x[m]的聯合機率分布(Joint Distribution),只和m和n的時間差有關,和其他參數都沒有關係。
另外,上述對於平穩過程的定義,在m等於n的情況下,也同樣會滿足上述情況,因此,如果是一個平穩隨機過程的話,應該也滿足以下條件:
![]()
也就是說,一個平穩過程的機率密度函數(PDF)在任意時間點n都是相同的,也就是說,這會是一個和當下時間點沒有關係(time independent)的函式。
因此,根據上面的定義,我們可以推導出,對於平穩過程的自相關函數(autocorrelation)也只和時間差有關,和本身的時間點沒有關係。如果假設時間差是k,則可以得到公式如下:
![]()
此外,藉由這些公式也可以得知,平穩過程的平均數(mean)和變異數(variance)也都和時間點n沒有關係,在任意時間點的值都是相同的,可以表示成如下的形式:
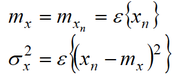
範例
舉例來說,白噪音,又稱為白雜訊(white noise)就是一個典型的平穩過程,而且它的時間是連續的,並且功率譜密度是常數,也就是說,它的每個頻段的功率是一樣的。雖然說鐃鈸的敲擊如果只有一下,則因為是能量會隨著時間衰減,而不是一個平穩過程,然而當它被打擊時,是有可能產生白雜訊的響應,假設它是在一個均勻穩定的卜瓦松過程(Poisson process)下敲擊的話,這個訊號則會形成白雜訊。
而如果是離散時間的平穩過程,同時又是在離散空間樣本下的話,則是有像是Bernoulli scheme的例子。
而在離散時間又是在連續空間樣本之下的話,則是有自回歸滑動平均模型(Autoregressive moving average model),這是研究時間序列的重要方法,是由自迴歸模型(AR模型)與滑動平均模型(MA模型)為基礎所「混合」構成。
此外,還可以假設Y是任意的隨機變數(Random variable),則同時定義一個時間數列{Xt},對於所有的t,有以下性質:
Xt = Y
而{Xt}就是一個平穩時間數列。
广义平稳(弱平穩)
信号处理中常用的弱平稳也被称为广义平稳(Wide-sense stationary,WSS)或者协方差平稳。WSS 随机过程仅仅要求一阶和二阶矩不随时间变化。
这样,一个 WSS 的连续时间随机过程 x(t) 有下述数学期望函数
- 1. E{x(t)}=mx(t)=mx(t+τ)∀τ∈R{displaystyle mathbb {E} {x(t)}=m_{x}(t)=m_{x}(t+tau ),,forall ,tau in mathbb {R} }
与相关函数
- 2. E{x(t1)x(t2)}=Rx(t1,t2)=Rx(t1+τ,t2+τ)=Rx(t1−t2,0)∀τ∈R.{displaystyle mathbb {E} {x(t_{1})x(t_{2})}=R_{x}(t_{1},t_{2})=R_{x}(t_{1}+tau ,t_{2}+tau )=R_{x}(t_{1}-t_{2},0),,forall ,tau in mathbb {R} .}
第一个属性表明数学期望函数 mx(t) 必须是常数。第二个属性表明相关函数仅仅与 t1{displaystyle t_{1}} 和 t2{displaystyle t_{2}} 之间的差值相关,并且可以仅仅用一个变量而不是两个变量来表示。这样,
- Rx(t1−t2,0),{displaystyle ,!R_{x}(t_{1}-t_{2},0),}
通常可以简化为
Rx(τ){displaystyle ,!R_{x}(tau )},其中:τ=t1−t2{displaystyle ,!tau =t_{1}-t_{2}}。
当使用线性、时不变(线性时不变系统)滤波器处理广义平稳随机信号的时候,将相关函数作为线性算子是很有帮助的。由于它是循环矩阵运算,只与两个变量之间的差值有关,所以它的特征函数是傅里叶级数复数指数函数。另外,由于线性时不变系统算子也是复指数函数,广义平稳随机信号的线性非时变处理非常易于操作——所有的运算都可以在频域进行。另外,根據線性非時變系統的特徵,也可以知道,當輸入訊號是一個廣義平穩過程時,輸出訊號也會是一個廣義平穩過程。因此,广义平稳假设在信号处理算法中得到了广泛应用。
二阶平稳过程
二阶平稳过程是指在实际使用中,仅需一对变量(2个)在时序变化中保持平稳特性时所提出的。二阶平稳过程的定义可以推广至N阶平稳过程,所谓严格平稳过程(SSS)具体表现为全阶平稳。
当概率密度函数的一阶和二阶表达式对于所有可能的t1{displaystyle t_{1}}, t2{displaystyle t_{2}} 和 Δ{displaystyle Delta } 满足以下条件时,被称为二阶平稳过程。
- fX(x1:t1)=fX(x1:t1+Δ),{displaystyle f_{X}(x_{1}:t_{1})=f_{X}(x_{1}:t_{1}+Delta ),,}
- fX(x1,x2:t1,t2)=fX(x1,x2:t1+Δ,t2+Δ),{displaystyle f_{X}(x_{1},x_{2}:t_{1},t_{2})=f_{X}(x_{1},x_{2}:t_{1}+Delta ,t_{2}+Delta ),,}
当其均值(mean)和相关函数(correlation function)都是有限的时候,这样的过程可以称为广义平稳(WSS),同时,一个广义平稳不一定是二阶平稳。
参见
- 循环平稳过程











